这里“MM”-马尔可夫模型,不是跟中国网络俗语“美眉”有关，而是跟俄国的“老司机”马尔可夫有关。

这位“老司机”全名叫安德雷·安德耶维齐·马尔可夫（Андрей Андреевич Марков），是俄国数学家。1874年18岁的马尔可夫考入圣彼得堡大学，师从切比雪夫（另一位俄国“老司机”，著名的切比雪夫定理-概率论与数理统计的基础），物理-数学博士，毕业后留校任教，圣彼得堡大学教授，圣彼得堡科学院院士。在概率论、数论、函数逼近论和微分方程等方面卓有成就。

马尔可夫模型概述：

马尔可夫模型MM（MarkovModel）是一种统计模型。它的原始模型马尔可夫链，由俄国数学家马尔可夫于1906年提出，将此一般化到可数无限状态空间是由柯尔莫果洛夫在1936年给出的。马尔可夫链是与马尔可夫过程紧密相关。马尔可夫过程是研究离散事件动态系统状态空间的重要方法，它的数学基础是随机过程理论。

马尔可夫性质：

此性质称为马尔可夫性质（Markov Property），亦称无后效性或无记忆性。

若X(t)为离散型随机变量，则马尔可夫性亦满足等式。

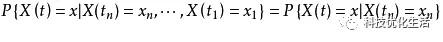
马尔可夫过程：

若随机过程{X(t), t属于T}满足马尔可夫性质，则称为马尔可夫过程。

比如，荷花池中一只青蛙的跳跃，液体中微粒所作的布朗运动，传染病受感染的人数，原子核中一自由电子在电子层中的跳跃，人口增长过程、闯迷宫的老鼠等都可视为马尔可夫过程。

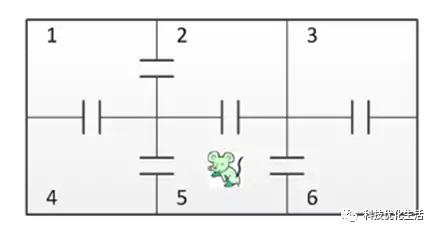
常见马尔可夫过程有：

(1)独立随机过程为马尔可夫过程。

(2)独立增量过程为马尔可夫过程。

(3)泊松过程为马尔可夫过程。

(4)维纳过程为马尔可夫过程。

(5)质点随机游动过程为马尔可夫过程。

跟朴素贝叶斯、支持向量机等机器学习算法不同，马尔可夫过程不必给处理的数据打标签。马尔可夫过程更侧重于处理控制或决策问题。

马尔可夫过程用于预测基本步骤：首先确定系统状态,然后确定状态之间转移概率,再进行预测,并对预测结果进行分析-若结果合理,则可提交预测报告,否则需检查系统状态及状态转移概率是否正确。

马尔可夫链：

马尔可夫链MC（Markov Chain）是指数学中具有马尔可夫性质的离散事件随机过程。该过程中，在给定当前知识或信息的情况下，过去对于预测将来是无关的。在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态。状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率。

时间和状态都离散的马尔可夫过程成为马尔可夫链MC。

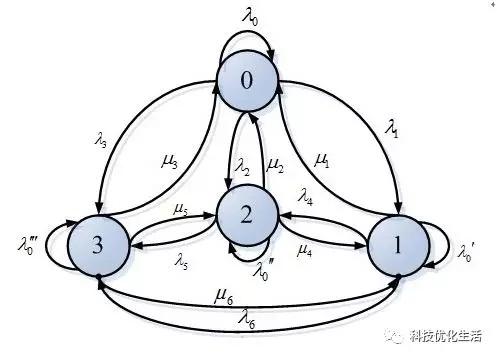
马尔可夫链原理：

马尔可夫链MC描述了一种状态序列，其每个状态值取决于前面有限个状态。马尔可夫链是具有马尔可夫性质的随机变量的一个数列。这些变量的范围，即它们所有可能取值的集合，被称为“状态空间”，而的值则是在时间n的状态。

马尔可夫链是与马尔可夫过程紧密相关。运用马尔可夫链只需要最近或现在的动态资料便可预测将来。

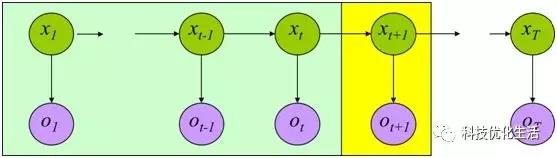
马尔可夫链性质：

马尔可夫链MC具有以下性质：

1）正定性：状态转移矩阵中的每一个元素被称为状态转移概率，由概率论知识可知，每个状态转移概率皆为正数，用公式即可表示为：

2）有限性：由概率论知识知，状态转移阵中的每一行状态转移阵中每行相加皆为1，用公式可表示为:

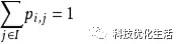
马尔可夫序列分类器：

序列分类器或序列标号器是给序列中的某个单元指派类或者标号的模型。诸如：词类标注、语音识别、句子切分、字素音位转换、局部句法剖析、语块分析、命名实体识别、信息抽取都属于序列分类。

马尔可夫序列分类器为：

1）显马尔可夫模型（VMM），又叫马尔可夫模型MM。

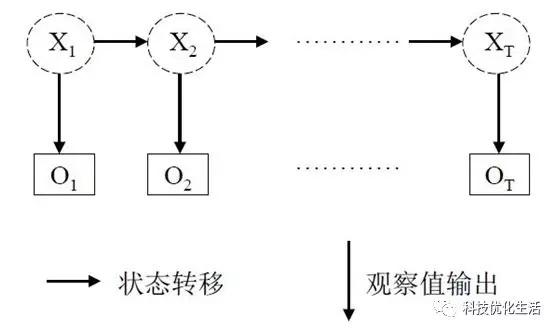
2）隐马尔可夫模型（HMM）,描述一个含有隐含未知参数的马尔可夫过程，是一个双重随机过程（包括马尔可夫链和一般随机过程）。

马尔可夫模型应用：

马尔可夫模型广泛应用在语音识别，词性自动标注，音字转换，概率文法等各个自然语言处理、算术编码、地理统计学、企业产品市场预测、人口过程、生物信息学（编码区域或基因预测）等应用领域。经过长期发展，尤其是在语音识别中的成功应用，使它成为一种通用的统计工具。

1）状态统计建模：马尔可夫链通常用来建模排队理论和统计学中的建模。还可作为信号模型用于熵编码技术等。马尔科夫链预测法是一种适用于随机过程的科学、有效的动态预测方法。马尔可夫链有众多的生物学应用，特别是人口过程，可以帮助模拟生物人口过程的建模。

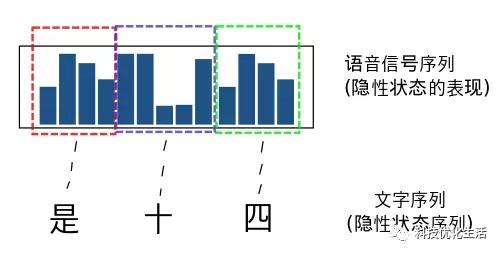
2）隐蔽马尔可夫模型（HMM）还被用于生物信息学，用以编码区域或基因预测。1980年代后半期，HMM开始应用到生物序列尤其是DNA的分析中。此后，在生物信息学领域HMM逐渐成为一项不可或缺的技术。到目前为止，隐马尔可夫模型（HMM）一直被认为是实现快速精确的语音识别系统的最成功的方法。复杂的语音识别问题通过隐含马尔可夫模型能非常简单地被表述、解决，让人们由衷地感叹数学模型之妙。

3）马尔科夫链蒙特卡罗方法（Markov Chain Monte Carlo）方法: 马尔科夫链蒙特卡罗MCMC是在朴素贝叶斯[请参见公众号“科技优化生活”之人工智能（29）]论框架下，通过计算机进行模拟的蒙特卡罗方法[请参见公众号“科技优化生活”之人工智能（31）]，该方法将马尔科夫链(MC)引入到蒙特卡罗（MC）模拟中，实现随着抽样分布随机模拟的进行而改变的动态模拟，弥补了传统的蒙特卡罗积分只能静态模拟的缺陷，是近年来广泛应用的统计计算方法。

结语:

马尔可夫模型（Markov Model）是一种统计模型。它的原始模型马尔可夫链，由俄国数学家马尔可夫于1906年提出。运用马尔可夫链只需要最近或现在的动态资料便可预测将来。马尔可夫链是与马尔可夫过程紧密相关。马尔可夫过程是研究离散事件动态系统状态空间的重要方法，它的数学基础是随机过程理论。马尔可夫模型在及人工智能之自然语言处理等领域应用广泛。

原创   张志荣