人工智能之CART算法
人工智能机器学习有关算法内容,请参见公众号“科技优化生活”之前相关文章。人工智能之机器学习主要有三大类:1)分类;2)回归;3)聚类。今天我们重点探讨一下CART算法。
继上两篇决策树算法之ID3算法[参见人工智能(41)]和ID3的改进算法-C4.5算法[参见人工智能(42)]后,本文继续讨论另一种二分决策树算法-CART算法。我们知道十大机器学习中决策树算法占有两席位置,即C4.5算法和CART算法,可见CART算法的重要性。下面重点介绍CART算法。
不同于ID3与C4.5,CART为一种二分决策树,是满二叉树。CART算法由Breiman等人在 1984 年提出,它采用与传统统计学完全不同的方式构建预测准则,它是以二叉树的形式给出,易于理解、使用和解释。由CART 模型构建的预测树在很多情况下比常用的统计方法构建的代数学预测准则更加准确,且数据越复杂、变量越多,算法的优越性就越显著。
CART算法既可用于分类也可用于回归。CART算法被称为数据挖掘领域内里程碑式的算法。
CART算法概念:
CART(Classification andRegression Tree) 分类回归树是一种决策树构建算法。CART是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。CART假设决策树是二叉树,内部结点特征的取值为“是”和“否”,左分支是取值为“是”的分支,右分支是取值为“否”的分支。这样的决策树等价于递归地二分每个特征,将输入空间即特征空间划分为有限个单元,并在这些单元上确定预测的概率分布,也就是在输入给定的条件下输出的条件概率分布。
CART算法既可以处理离散型问题,也可以处理连续型问题。这种算法在处理连续型问题时,主要通过使用二元切分来处理连续型变量,即特征值大于某个给定的值就走左子树,或者就走右子树。
CART算法组成:
CART算法组成如下:
1)决策树生成:基于训练数据集生成决策树,生成的决策树要尽量大;自上而下从根开始建立节点,在每个节点处要选择一个最好(不同算法使用不同指标来定义"最好")的属性来分裂,使得子节点中的训练数据集尽量的纯。
2)决策树剪枝:用验证数据集对已生成的树进行剪枝并选择最优子树,这时损失函数最小作为剪枝的标准。这里用代价复杂度剪枝CCP(Cost-Complexity Pruning)。
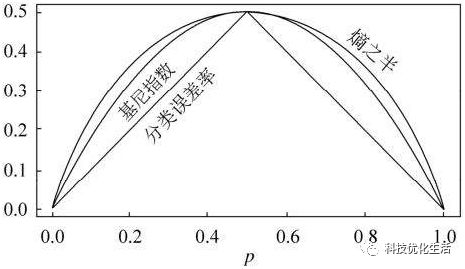
决策树的生成就是通过递归地构建二叉决策树的过程,对回归树用平方误差最小化准则,对分类树用基尼指数最小化准则,进行特征选择,生成二叉树。
CART决策树生成:
1)回归树生成
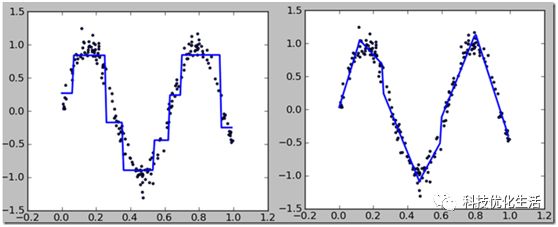
回归树采用均方误差作为损失函数,树生成时会递归的按最优特征与最优特征下的最优取值对空间进行划分,直到满足停止条件为止,停止条件可以人为设定,比如当切分后的损失减小值小于给定的阈值 ε,则停止切分,生成叶节点。对于生成的回归树,每个叶节点的类别为落到该叶节点数据的标签的均值。
回归树为一棵二叉树,每次都是按特征下的某个取值进行划分,每一个内部节点都是做一个对应特征的判断,直至走到叶节点得到其类别,构建这棵树的难点在于如何选取最优的切分特征与切分特征对应的切分变量。
回归树与模型树既可以处理连续特征也可以处理离散特征。
回归树生成算法如下:
输入:训练数据集 D={(x1,y1),(x2,y2),…,(xN,yN)}
输出:回归树 T
1)求解选择切分特征 j 与切分特征取值 s ,j 将训练集 D 划分为两部分,R1 与R2 ,依照(j,s)切分后如下:
R1(j,s)={xi|xji≤s} R2(j,s)={xi|xji>s}
c1=1N1∑xi∈R1yi c2=1N2∑xi∈R2yi
2)遍历所有可能的解(j,s),找到最优的 (j*,s*) ,最优的解使得对应损失最小,按照最优特征(j*,s*)来切分即可。
Min { ∑ (yi–c1)^2 +∑ (yi–c2)^2 }
j,s xi∈R1 xi∈R2
3)递归调用 1)和2),直到满足停止条件。
4)返回决策树 T。
回归树主要采用了分治策略,对于无法用唯一的全局线性回归来优化的目标进行分而治之,进而取得比较准确的结果,但分段取均值并不是一个明智的选择,可以考虑将叶节点设置为一个线性函数,这便是所谓的分段线性模型树。实验表明:模型树效果比回归树的效果要好一些。模型树只需在回归树的基础上稍加修改即可,对于分到叶节点的数据,采用线性回归的最小均方损失来计算该节点的损失。
2)分类树生成
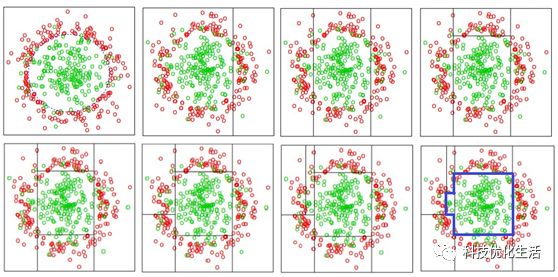
分类树是CART中用来分类的,不同于 ID3 与 C4.5,CART分类树采用基尼指数来选择最优的切分特征,而且每次都是二分。
基尼指数是一个类似与熵的概念,对于一个有 K 种状态对应的概率为 p1,p2,…,pK的随机变量 X ,其基尼指数Gini定义如下:
Gini(X)=∑pk(1?pk)=1?∑kp2k
k k
在已知特征 A条件下集合 D 的基尼指数:
Gini(D,A)=(|D1|/|D|)*Gini(D1)+(|D2|/|D|)*Gini(D2)
Gini(D,A)取值越大,样本的不确定性也越大,这一点与熵类似,所以选择特征 A 的标准是 Gini(D,A) 的取值越小越好。
分类树生成算法如下:
输入:训练数据集 D={(x1,y1),(x2,y2),…,(xN,yN)},停止条件
输出:分类树 T
1)利用特征 A 的取值 a 将数据分为两部分,计算 A=a时的基尼系数:
Gini(D,A)=(|D1|/|D|)*Gini(D1)+(|D2|/|D|)*Gini(D2)
2)对整个数据集中所有的可能特征 A 以及其可能取值 a 选取基尼系数最小的特征 A* 与特征下的取值 a*,来将数据集切分,将数据 D1、D2 分到两个子节点中去。
3)对子节点递归调用 1)和2) ,直至满足停止条件
4)返回 CART 树 T
该算法停止条件可以是节点中的样本数不能小于给定阈值,或者样本集的基尼系数小于给定阈值,或者没有更多的特征。
3)剪枝
CART需要对生成的树进行剪枝,避免模型过度拟合训练数据,剪枝时使用的损失函数如下:
Ca(T)=C(T)+a|T|
C(T)为树 T 对训练数据的误差,可以用基尼系数或者均方损失来表示,a≥0 代表一个权衡训练数据损失 C(T)与总节点数 |T|的参数,Ca(T) 代表了树 T 的整体损失,对于固定的 a,一定存在一个确定的使得 Ca(T)最小的子树,当 a偏大时, |T| 偏小,树 T 的规模偏小,反之,树 T 的规模偏大,Breiman 等人采用递归的方法对 CART 进行剪枝,将 a从小增大 0=a0<a1<…<an,如此产生的区间 a∈[ai,ai+1), i=1,2,…,n用对应此区间的 a 产生一系列的子树序列 {T0,T1,…,Tn}这里 Ti+1总是由 Ti 剪枝后产生。
剪枝算法如下:
输入:CART 生成树 T0
输出:剪枝后的最优树 T*
1)设 k=0 , T=T0 ,a=+∞
3) 自下而上的对内部节点 t 计算:
g(t)=[Ct?C(Tt)]/(|Tt|?1)
a=min(a,g(t))
4) 自上而下的访问内部节点 t ,对最小的 g(t)=a进行剪枝,并对叶节点 t 以多数表决形式决定其类别,得到树 T
5) k=k+1, ak=a,Tk=T
6) 如果 T 为非单节点树,回到4)
7) 对于产生的子树序列 {T0,T1,…,Tn}分别计算损失,得到最优子树 T*并返回.
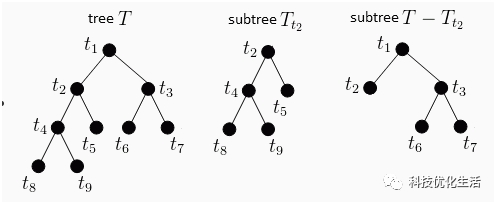
剪枝后的树便是所需要的CART决策树。
CART优点:
1) 可以生成可以理解的规则;
2) 计算量相对来说不是很大;
3) 可以处理连续和种类字段;
4)决策树可以清晰的显示哪些字段比较重要。
CART缺点:
1) 对连续性的字段比较难预测;
2) 对有时间顺序的数据,需要很多预处理的工作;
3)当类别太多时,错误可能就会增加的比较快;
4)一般的算法分类的时候,只是根据一个字段来分类。
CART应用场景:
CART算法既可以处理离散型问题,也可以处理连续型问题。CART算法是一种非常有趣且十分有效的非参数分类和回归方法。它通过构建二叉树达到预测目的。它已在统计、数据挖掘和机器学习领域中普遍使用,是一种应用广泛的决策树算法。
结语:
CART 模型最早由Breiman 等人提出,它采用与传统统计学完全不同的方式构建预测准则,它是以二叉树形式给出,易于理解、使用和解释。由CART 模型构建的预测树在很多情况下比常用的统计方法构建的代数学预测准则更加准确,且数据越复杂、变量越多,CART算法优越性就越显著。模型的关键是预测准则的构建。CART算法在统计、数据挖掘和机器学习等领域得到广泛应用。
------以往文章推荐------
机器学习
深度学习
人工神经网络
决策树
随机森林
强化学习
迁移学习
遗传算法
朴素贝叶斯
支持向量机
蒙特卡罗方法
马尔科夫模型
Hopfield神经网络
回归模型
K邻近算法
卷积神经网络
受限玻尔兹曼机
循环神经网络
长短时记忆神经网络
Adaboost算法
ID3算法
C4.5算法

最新活动更多
-
3月27日立即报名>> 【工程师系列】汽车电子技术在线大会
-
即日-4.22立即报名>> 【在线会议】汽车腐蚀及防护的多物理场仿真
-
4月23日立即报名>> 【在线会议】研华嵌入式核心优势,以Edge AI驱动机器视觉升级
-
4月25日立即报名>> 【线下论坛】新唐科技2025新品发布会
-
在线会议观看回放>>> AI加速卡中村田的技术创新与趋势探讨
-
即日-5.15立即报名>>> 【在线会议】安森美Hyperlux™ ID系列引领iToF技术革新











 分享
分享















发表评论
请输入评论内容...
请输入评论/评论长度6~500个字
暂无评论
暂无评论