简单一文助你理解DBSCAN是什么
一般说到聚类算法,大多数人会想到k-means算法,但k-means算法一般只适用于凸样本集,且需要预先设定k值,而DBSCAN聚类既可以用于凸样本集,也可以用于非凸样本集,也不需要提前设定簇族数。关于凸样本集的解释如下图所示。

关于DBSCAN聚类,它是基于密度的聚类,一般通过样本间的紧密程度来进行聚类,将紧密相连的一类样本化为一类,直至遍历所有样本点。
而DBSCAN聚类有下面几个定义。
1.ε-邻域:有一个样本点x1,以x1为圆心,半径为ε的一个范围
2.min_sample(最小样本点数):在样本点x1的ε-邻域内的所有样本点总数n;如果n>=min_sample,样本点成为核心点,否则为非核心点。而非核心又分为边界点和噪声点。他们的区别在于其ε-邻域内是否存在核心点,如果存在则为边界点,否则为噪声点。
3.密度直达:有样本点x1位于x2的ε-邻域内,且x2为核心点,则称x1由x2密度直达。
4.密度可达:有样本点x1位于x2的ε-邻域内,且x1和x2均为核心点,则称x1和x2密度可达。
5.密度相连:有非核心点x1和x2均在核心点x3的ε-邻域内,则称x1和x2密度相连。所有密度相连的样本点组成一个集合。
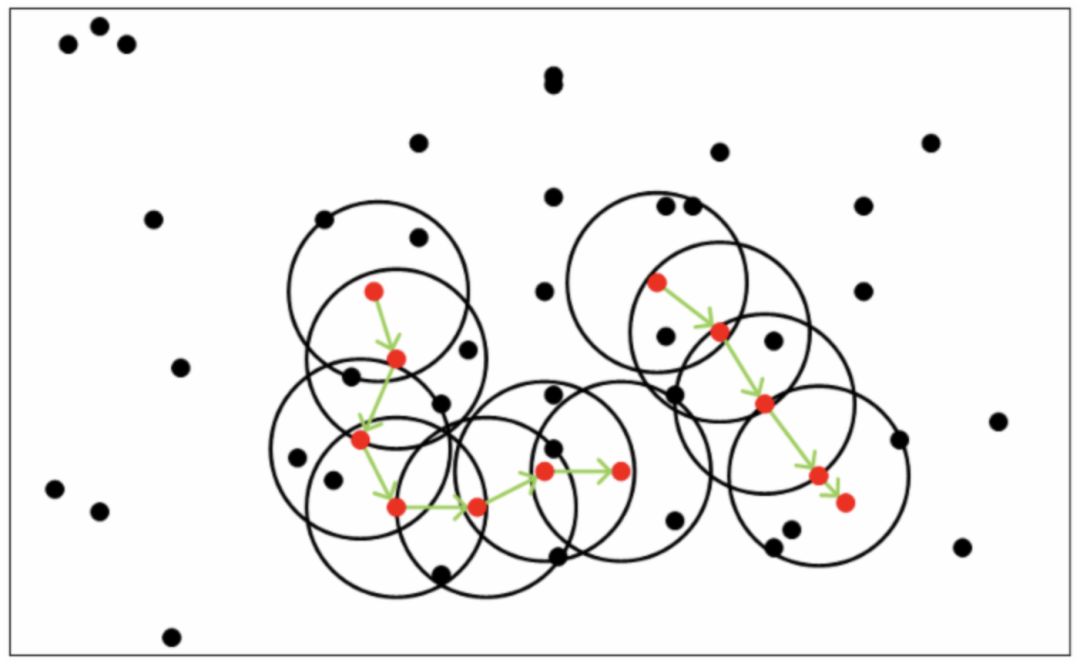
上图中的红色点为核心点,黑色点为非核心点(包括边界点和噪音点)。一共有两组密度可达,第一组(左边)有七个核心点,其集合包括七个核心点以及各个ε-邻域内的所有边界点。第二组(右边)有五个核心点,其集合包括五个核心点以及各个ε-邻域内的所有边界点。当所有非噪声点均在不同集合内时,聚类结束。
因此,可以将DBSCAN聚类的流程定义如下:
有数据集X={x1,x2,...,xn},设置好min_sample和邻域半径值。
1.遍历数据集,将各个样本点间的距离保存到一个矩阵中;
2.遍历数据集,将所有的核心点,以及各个核心点邻域内的样本点找出;
3.如果核心点间的距离小于半径值,则将两个核心点连接到一起;最终会形成若干簇族;
4.将所有边界点分配到离他最近的核心点;
5.直至所有非噪音点完成分配,算法结束。
python实现
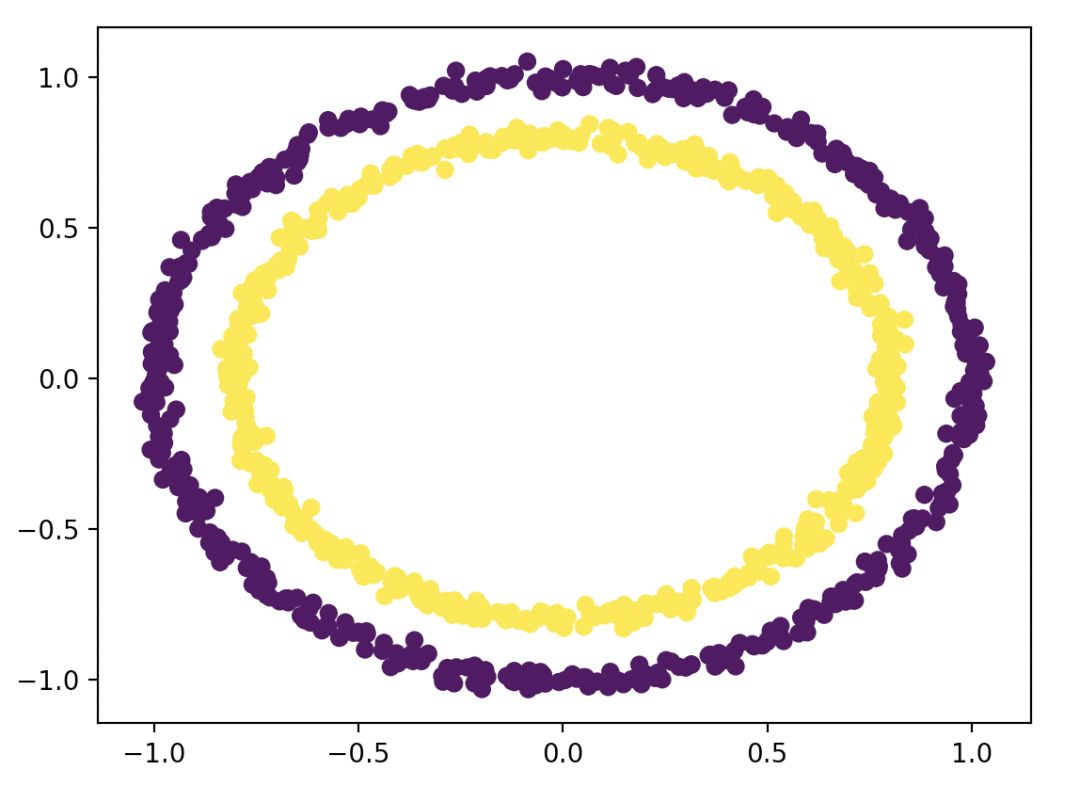
用的是sklearn库自带的数据集---make_circles。散点图如下。
根据上面定义的流程,开始写代码啦。
首先要得到各个样本点间的距离:
def dis(self,va,vb): s=(va-vb) f=sqrt(s*s.T) return f[0,0]
def get_distance(self,dataset): m,n=shape(dataset)[0],shape(dataset)[1] dataset=mat(dataset) dis=mat(zeros((m,m))) for i in range(m): for j in range(i,m): dis[i,j]=self.dis(dataset[i,],dataset[j,]) dis[j,i]=dis[i,j] return dis
然后找到所有的核心点,以及各个核心点邻域内的所有样本点集合。
def find_core_point(self,dismatrix): core_point=[] core_point_dict={} m=shape(dismatrix)[0] for i in range(m): ind=[] for j in range(m): if dismatrix[i,j]<self.eps: ind.append(j) if len(ind)>=self.min_sample: core_point.append(i) core_point_dict[str(i)]=ind core_point_core={} for key,value in core_point_dict.items(): o=[] for i in value: if i in core_point: o.append(i) core_point_core[key]=o return core_point,core_point_dict,core_point_core其中core_point是一个列表,存储所有的核心点core_point_dict是一个字典,key为核心点,value为该核心点邻域内的所有样本点集合core_point_core是一个字典,key为核心点,value为该核心点邻域内所有核心点集合
接下来就是找出密度直达点集合,也就是在邻域内的核心点集合
def join_core_point(self,core_point,core_point_dict,core_point_core): labels=array(zeros((1,len(core_point)))) num=1 result={} result[str(num)]=core_point_core[str(core_point[0])] for i in range(1,len(core_point)): q=[] for key,value in result.items(): r=self.get_same(core_point_core[str(core_point[i])],value) if r: q.append(key) if q: n=result[q[0]].copy() n.extend(core_point_core[str(core_point[i])]) for i in range(1,len(q)): n.extend(result[q[i]]) del result[q[i]] result[q[0]]=list(set(n)) else: num=num+1 result[str(num)]=core_point_core[str(core_point[i])] return result
再将所有边界点划分到其最近的核心点一簇并画出。
def ddbscan(self,data, label): m=shape(data)[0] dismatrix=self.get_distance(data) types=array(zeros((1,m))) number=1 core_point, core_point_dict,core_point_core=self.find_core_point(dismatrix) if len(core_point): core_result=self.join_core_point(core_point,core_point_dict,core_point_core) for key,value in core_result.items(): k=int(key) for i in value: types[0,i]=k for j in core_point_dict[str(i)]: types[0, j] = k print(types) newlabel=types.tolist()[0] data=array(data) q=list(set(newlabel)) print(q) colors = ['r', 'b', 'g', 'y', 'c', 'm', 'orange'] for ii in q: i=int(ii) xy=data[types[0,:]==i,:] plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=colors[q.index(ii)], markeredgecolor='w', markersize=5) plt.title('DBSCAN' ) plt.show()
最后的结果图如下:
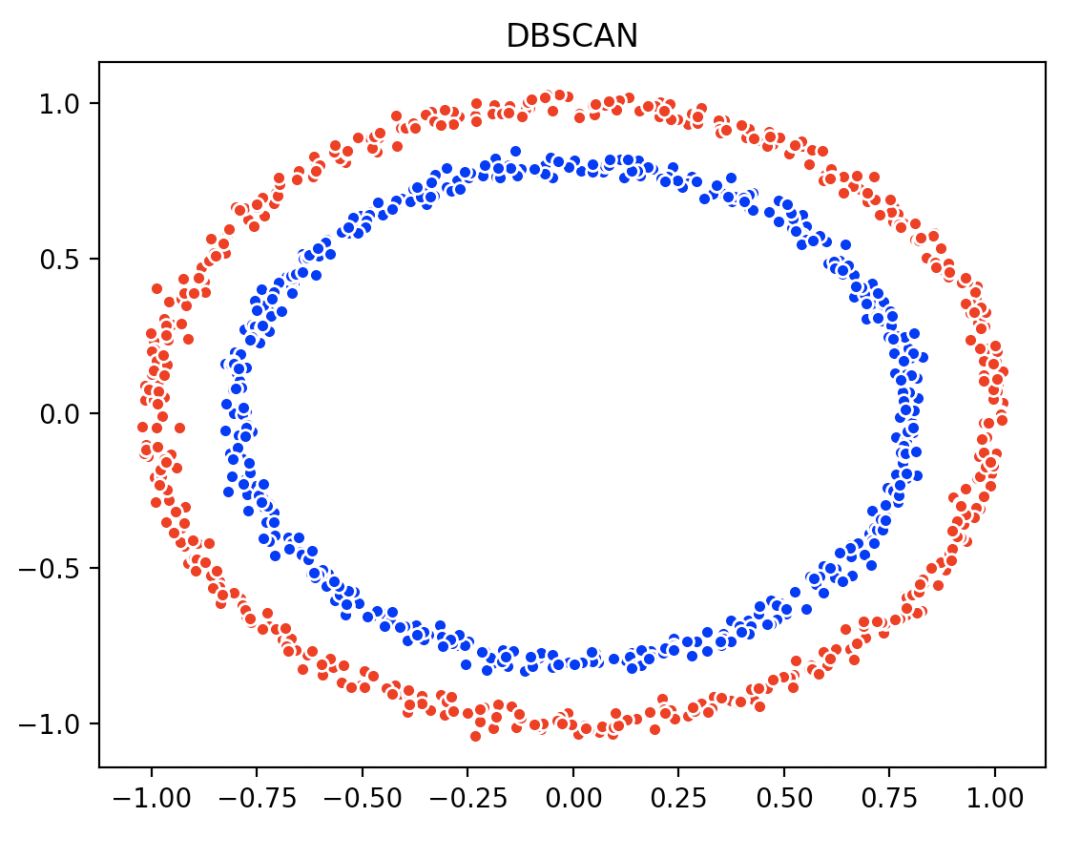
虽然效果不错,但自己写的就是比较辣鸡,一共用了10.445904秒;如果真的要用这个算法的话,不推荐大家用自己写的,事实上sklearn库就有DBSCAN这个函数,只需要0.0284941秒。
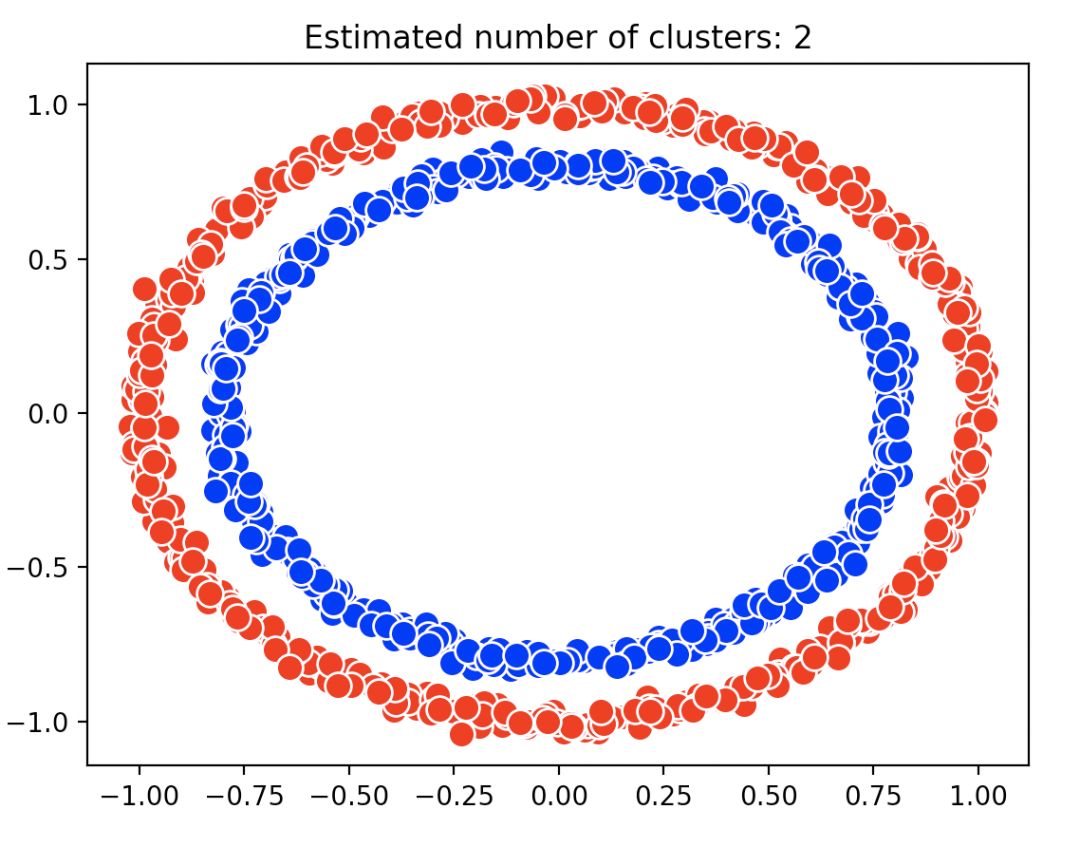
效果如上所示。而且代码也只有几行。代码复制于(http://itindex.net/detail/58485-%E8%81%9A%E7%B1%BB-%E7%AE%97%E6%B3%95-dbscan)
def skdbscan(self,data,label): data = array(data) db = DBSCAN(eps=self.eps, min_samples=self.min_sample, metric='euclidean').fit(data) core_samples_mask = zeros_like(db.labels_, dtype=bool) core_samples_mask[db.core_sample_indices_] = True labels = db.labels_ n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) unique_labels = set(labels) colors = ['r', 'b', 'g', 'y', 'c', 'm', 'orange'] for k, col in zip(unique_labels, colors): if k == -1: col = 'k' class_member_mask = (labels == k) xy = data[class_member_mask & core_samples_mask] plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col, markeredgecolor='w', markersize=10) plt.title('Estimated number of clusters: %d' % n_clusters_) plt.show()
关于DBSCAN这个函数有几个要注意的地方:
DBSCAN(eps=0.1, min_samples=5, metric='euclidean',
algorithm='auto', leaf_size=30, p=None, n_jobs=1)
核心参数:
eps: float-邻域的距离阈值
min_samples :int,样本点要成为核心对象所需要的 ?-邻域的样本数阈值
其他参数:
metric :度量方式,默认为欧式距离,可以使用的距离度量参数有:
欧式距离 “euclidean”
曼哈顿距离 “manhattan”
切比雪夫距离“chebyshev”
闵可夫斯基距离 “minkowski”
带权重闵可夫斯基距离 “wminkowski”
标准化欧式距离 “seuclidean”
马氏距离“mahalanobis”
自己定义距离函数
algorithm:近邻算法求解方式,有四种:
“brute”蛮力实现
“kd_tree” KD树实现
“ball_tree”球树实现
“auto”上面三种算法中做权衡,选择一个拟合最好的最优算法。
leaf_size:使用“ball_tree”或“kd_tree”时,停止建子树的叶子节点数量的阈值
p:只用于闵可夫斯基距离和带权重闵可夫斯基距离中p值的选择,p=1为曼哈顿距离, p=2为欧式距离。如果使用默认的欧式距离不需要管这个参数。
n_jobs :CPU并行数,若值为 -1,则用所有的CPU进行运算
DBSCAN聚类的优缺点
优点:
可以很好的发现噪声点,但是对其不敏感;
可以对任意形状的稠密数据进行聚类;
缺点:
1.需要设定min_sample和eps;不同的组合差别非常大;
2.数据量很大时,效率会特别低,收敛时间很长;
3.对于密度不均匀,聚类间差距很大的数据集效果很差。
最后,送一个基于DBSCAN聚类的笑脸给大家。可以去这个网站自行尝试。
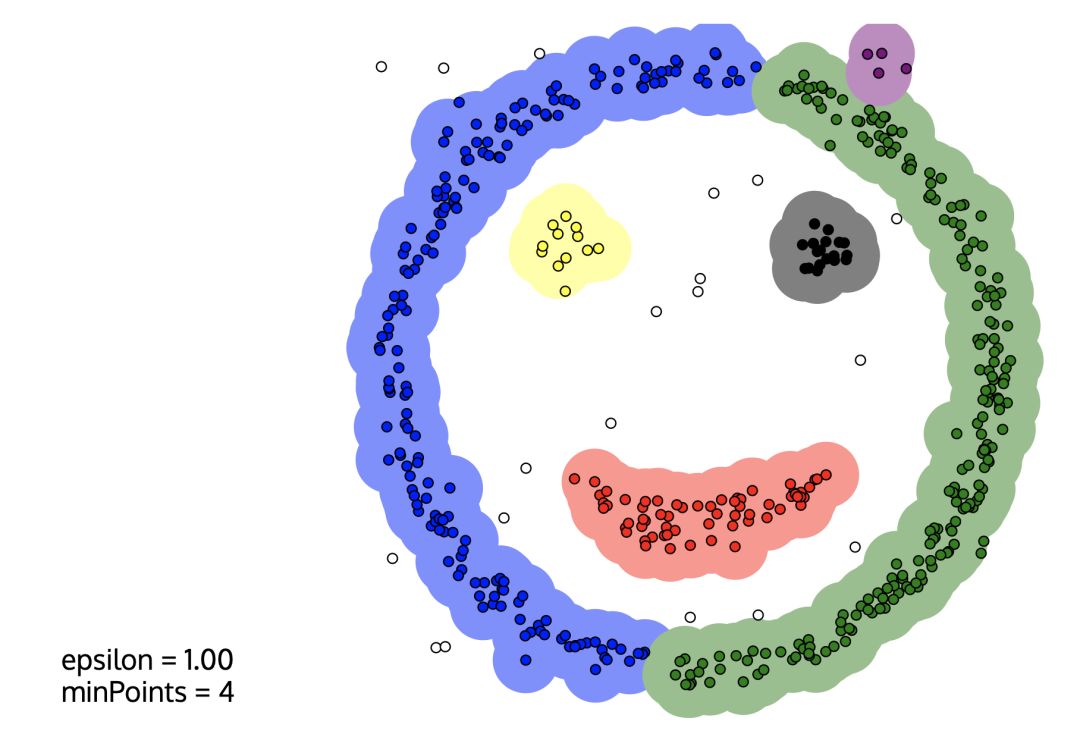
文章到这里就暂时告一段落啦,小伙伴们有没有收获满满咧?
------------------- End -------------------

最新活动更多
-
3月27日立即报名>> 【工程师系列】汽车电子技术在线大会
-
4月30日立即下载>> 【村田汽车】汽车E/E架构革新中,新智能座舱挑战的解决方案
-
5月15-17日立即预约>> 【线下巡回】2025年STM32峰会
-
即日-5.15立即报名>>> 【在线会议】安森美Hyperlux™ ID系列引领iToF技术革新
-
5月15日立即下载>> 【白皮书】精确和高效地表征3000V/20A功率器件应用指南
-
5月16日立即参评 >> 【评选启动】维科杯·OFweek 2025(第十届)人工智能行业年度评选











 分享
分享



















发表评论
请输入评论内容...
请输入评论/评论长度6~500个字
暂无评论
暂无评论