如图所示，我们没有太多异常数据，所以，如果我们从75％的值开始，会是比较好的结果，但为了安全起见，我会从平均值开始。所以我们将从平均值和更低的概率范围开始检查这个范围内每个概率的f1分数。首先，定义一个函数来计算真正例、假正例和假反例：def tpfpfn（ep）：

   tp， fp， fn ＝ 0， 0， 0
   for i in range（len（y））：
       if p［i］ ＜＝ ep and y［i］［0］ ＝＝ 1：
           tp ＋＝ 1
       elif p［i］ ＜＝ ep and y［i］［0］ ＝＝ 0：
           fp ＋＝ 1
       elif p［i］ ＞ ep and y［i］［0］ ＝＝ 1：
           fn ＋＝ 1
   return tp， fp， fn

列出低于或等于平均概率的概率。eps ＝ ［i for i in p if i ＜＝ p．mean（）］

检查一下列表的长度len（eps）

输出：133

根据前面讨论的公式定义一个计算f1分数的函数：def f1（ep）：
   tp， fp， fn ＝ tpfpfn（ep）
   prec ＝ tp／（tp ＋ fp）
   rec ＝ tp／（tp ＋ fn）
   f1 ＝ 2＊prec＊rec／（prec ＋ rec）
   return f1

所有函数都准备好了！现在计算所有epsilon和我们之前选择的概率值范围的f1分数。f ＝ ［］
for i in eps：
   f．append（f1（i））
f
输出：［0．14285714285714285，
0．14035087719298248，
0．1927710843373494，
0．1568627450980392，
0．208955223880597，
0．41379310344827586，
0．15517241379310345，
0．28571428571428575，
0．19444444444444445，
0．5217391304347826，
0．19718309859154928，
0．19753086419753085，
0．29268292682926833，
0．14545454545454545，

这是f分数表的一部分，它的长度是133。f分数通常在0到1之间，其中f1得分越高越好，所以，我们需要从刚才计算的f分数列表中取f的最高分数。现在，使用“argmax”函数来确定f分数值最大值的索引。np．array（f）．argmax（）
输出：131

现在用这个索引来得到阈值概率。e ＝ eps［131］

e

输出：6．107184445968581e－05

找出异常实例现在我们有了临界概率，可以从中找出我们训练数据的标签了。如果概率值小于或等于该阈值，则数据为异常数据，否则为正常数据。我们将正常数据和异常数据分别表示为0和1，label ＝ ［］
for i in range（len（df））：
   if p［i］ ＜＝ e：
       label．append（1）
   else：
       label．append（0）
label
输出：［0，
0，
0，
0，
0，
0，
0，
0，
0，
0，

这是标签列表的一部分。我将在上面的训练数据集中添加此标签：df［＇label＇］ ＝ np．array（label）

df．head（）

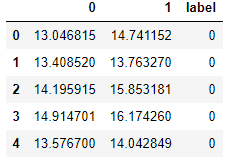
我在标签为1的地方用红色绘制数据，在标签为0的地方用黑色绘制，得到以下结果。

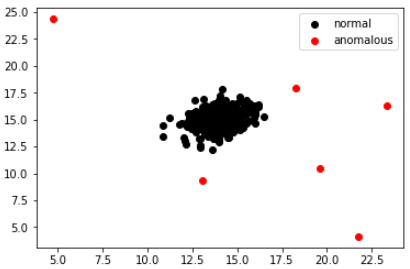
我们可以看到红色的数据明显是异常值。结论本文我们一步一步地解释了开发异常检测算法的整个过程，如果你通过阅读本文无法理解算法的过程，建议你运行每一段代码来加强理解。