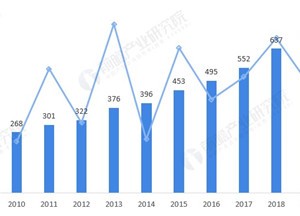
图3：101名正常人血清肌红蛋白的频数分布直方图

根据表1的资料，以各组段红细胞含量为横坐标，人数（频数）为纵坐标可绘制频数分布直方图，如图1。图2、图3也是根据相应的频数分布表绘制而成，我们可以更为形象和直观的发现数据的分布规律。

3、频数表和频数分布图的用途——发现数据分布规律

3．1 描述频数分布的类型    频数分布的类型可分为对称分布和偏态分布两种。若各组段的频数以频数最多组段为中心左右两侧大体对称，则认为该资料是对称分布（表1及图1）；反之，则认为是偏态分布（图2、图3）。图2频数最多组段（21～）右侧的组段数多于左侧的组段数，频数向右侧拖尾，称右偏态分布（skewed to the right distribution）也称正偏态分布（positive skewness distribution）。图3频数最多组段（30～ ）左侧的组段数多于右侧的组段数，频数向左侧拖尾，称左偏态分布（skewed to the left distribution），也称负偏态分布（negative skewness distribution）。

3．2 描述频数分布的特征     如在图2中，我们可以发现主要的2点特征：①数据变异的范围在0～45mmol／L之间；②有一定的规律，数据主要集中在20～30组段之间。数值较大的值多于数值较小的值，左右分布并不对称。

3．3 频数分布表可用发小一些异常值，如特别小的值或特别大的值。

3．4 频数分布表可用于发现数据分布规律，便于做进一步统计分析和处理

二、 计量资料的集中趋势

（1）均数（算术均数、几何均数）算数均数（mean）    均值是一个平均数，所以均值的计算方法是将一个分布中的所有取值加总起来除以取值的个数。如果一个分布中有10个取值，那么将所有取值加起来之后再除以10即可。可以利用原始数据进行计算，也可以利用频数分布表进行计算，但是其中的原理都是一样的，即计量资料中某一变量取值的总和除以个数。适用于资料符合正态分布的计量资料，公式可以表示如下：

几何均数（geometric mean）    用于一组经过对数转换后成对称分布的变量值在数量上的平均水平，在医学上常见的是免疫学的指标，其计算公式为：

例1，某地5例微丝蚴血症患者治疗7年后用间接受光抗体试验测得其抗体滴度倒数分别为10、20、40、40、16，求几何均数。

故5份血清抗体效价的平均滴度为1：34．8。

对于频数表资料，几何均数的计算公式为：

（2） 中位数与百分位数中位数     中位数（median）是将n个变量值从小到大排列，位置居于中间的那个数。当n为奇数时取位次居中的变量值，当n为偶数时取位次居中的两个变量值的均数。它适用于各种分布类型的资料，尤其是偏态分布资料和一端或两端无确切数值的资料。其计算公式为：

例3：试计算表2某医院1123名产后出血孕妇人工流产次数的中位数。对于离散型变量资料，因为n＝ 1123，故中位数是从小到大排序后居于（n＋ 1）／2＝（1123＋ 1）／2＝ 562位的观察值。据表2，排在第 1～402 位的观察值均为“0”，其累计频率为35．80％；排在403 ～732位的观察值＂1”，其累计频率为65．18％，余类推。第562位数属于第二个变量值，即人流次数为“1”，故某医院1123名产后出血孕妇人工流产次数的中位数为M＝X（562） ＝1 。

百分位数     百分位数（percentile），是一种位置指标， 用Px来表示，读作第x百分位数。一个百分位数 Px将全部变量值分为两部分，在Px处若无相同变量值，则在不包含Px的全部变量值中有x％的变量值小于它，（100－x％）变量值大于它。故百分位数是一个界值，其最重要用途是用来确定医学参考值范围（reference range），后面我们会谈到。中位数实际上是第50百分位数，是百分位数中的一个特殊值。

例4：对某医院细菌性痢疾治愈者的住院天数统计，119名患者的住院天数从小到大的排列如下，试求第5百分位数和第99百分位数。患者：1 2 3 4 5 6 7 8…116 117 118 119住院天数：1 1 2 2 2 3 4 4 5…39 40 40 42（119＋1）x5％＝6，故P（5）＝X（6）＝3（天）（119＋1）x 99％＝118．8， 故P（99）在118位和119位之间，通过对应的公式计算出为41．6（天），详细的计算公式我就不列出来了，因为现在都不会手动计算啦，我们掌握它的应用和意义更为重要。故我们解读一下这里涉及的P（5）和P（99）的意义：P（5）的意义是该医院有5％的细菌性痢疾治愈者的住院天数少于3天，或者说有95％的细菌性痢疾治愈者的住院天数多于3天。P（99）的意义是绝大多数（99％）细菌性痢疾治愈者的住院天数少于41．6天。

利用频数分布表计算百分位数：例5： 某地118名链球菌咽喉炎患者的潜伏期频数表见表3第（1）、（2）栏，求中位数及第25位、第75位百分位数。

中位数对应的累计频率是50％，对表中第（4）栏从上到下读累计频率，小于48天的累计频率为44．9％，小于60天的累计频率为65．3，故中位数所在组段为“48～”，n＝ 118（样本总量），L50 ＝ 48（P50所在组段的下界），i50＝ 12（组间距），f50＝24（P50所在组段的样本量）， L ＝53（P50前一组段的累积频数），带入计算公式得：M＝P50＝48＋12／24（118x50％－53）＝51（天）

同样的计算原理，我们可以计算出P25和P75：P25＝36＋12／32（118x25％－21）＝39．2（天）P75＝ 60＋12／18（118x75％－77）＝67．7（天）

对于离散变量的频数表资料，第X百分位数为Px所在变量值处的变量值，如对表2资料有P95＝3；若每个组有几个变量值，则必须根据原始数据用直接法求Px。

众数     众数（mode）是使用最少的集中趋势指标，因为它提供的信息量最少。众数只是指出分布中最常出现的取值，或者具有最高频数的取值。

三、 计量资料的离散趋势

离散（dispersion）趋势指的是计量资料所有变量值偏离中心位置的程度，要全面刻画一组数据（变量值）的数量特征，除计算平均指标外，还必须计算反映离散程度的指标。描述离散程度的常用指标有极差、四分位数间距、方差、标准差和变异系数。

极差（Range）

如前所述，极差即一组变量值的最大值与最小值之差。极差计算简便，概念清晰，因而应用比较广泛，如说明传染病、食物中毒的最长、最短潜伏期等．

例6：试计算下面三组同龄男孩的身高（cm）均数和极差。甲组：90 95 100 105 110   乙组：96 98 100 102 104   丙组：96 99 100 101 104  计算得出：

比较以上三组数据发现，虽然三组均数相等，但极差却不尽相间，甲组5个儿童身高差异20 cm，乙组和丙组只有8 cm。我们可以很容易的得出结论，若仅比较三组的均数，而不比较个体差异的大小，不能全面反映三组儿童身高。

用极差来描述数据的变异程度并不全面。仅能反映最大值与最小值的差值，而不论其他数值的情况。

四分位数间距

四分位数（quartile）是把全部变量值分为四部分的分位数，即第1四分位数（QL＝P25）、第2四分位数（M＝P50）、第3四分位数（QU＝P75）。四分位数间距（quartile range）是由第3四分位数和第1四分位数相减而得，记为QR。它一般和中位数起描述偏态分布资料的分布特征。

方差与标准差

方差（variance）也称均方差（mean square deviation），反映组数据的平均离散水平。离均差平方和除以N得到了方差，总体方差用σ2。常与均数一起描述正态分布资料的分布特征。其计算公式如下：

例7：续例6，试计算下面三组同龄男孩的身高（cm）标准差。甲组：90 95 100 105 110   乙组：96 98 100 102 104  丙组：96 99 100 101 104  带入公式得：S甲＝7．9cm，S乙＝3．2cm，S丙＝2．9cm由于丙组的标准差较小，说明组间变异程度较小，故可以认为其均数的代表性较其他组要好。

变异系数

变异系数（Coefficient of variation）记为CV，多用于观察指标单位不同时，如身高与体重的变异程度的比较；或均数相差较大时，如儿童身高与成人身高变异程度的比较。其计算公式为：

例8：某地7岁男孩身高的均数为123．10 cm，标准差为4．71 cm；体重均数为22．92 kg，标准差为2．26kg。此处不能因为4．71＞2．26，就说身高的变异比体重要大，而要考虑到两者的单位不同，无法直接比较，故采用变异系数来解决这类问题，它实质上是一个相对变异指标，无单位。上述7岁男孩身高、体重的变异系数分别为：

通过比较，说明该地7岁男孩体重的变异大于身高的变异，或者说身高比体重的变异小。

总结：在这一小节中，我们详细的谈及了描述计量资料集中趋势和离散趋势的指标。也谈到了它们的应用场所，总结起来就是“正态分布资料：均值±标准差；偏态分布资料：中位数，四分位数间距”，在以后的学习中，我们看到文献中的图表，看到其描述的方式，就应该迅速在脑海里反映出其对应的资料的分布情况；反之亦然，见到不同分布的资料，我们应该知道用那些指标对其进行描述。

如上图文献［Prevalence and related factors of chronic kidney disease （CKD） among long－lived individuals （LLI） over 95 years of age］中的表1，我们可以看到连续型变量使用（均数±标准差）的形式进行统计描述；而分类变量使用的是构成比的形式进行描述。因为在实际工作和生活中，偏态分布的例子极少，而作者研究中仅用连续变量和分类变量区分变量类型，故未展示（中位数，四分位间距）这一表现形式。

参考资料：

1．人民卫生出版社《医学统计学》第4版  孙振球 徐勇勇 著2．中国人民大学出版社《白话统计学》第3版   蒂莫西．C．厄丹（Timothy C．Urdan）著，彭志文译3．Zujun et al．，2015，Prevalence and related factors of chronic kidney disease （CKD） among long－lived individuals （LLI） over 95 years of age，Archives of Gerontology and Getratrics，Volume 60，Issue2，March–April 2015， Pages 354－358