CVPR 2020 最佳论文提名 | 神经网络能否识别镜像翻转
为了深入了解人脸的视觉手性现象,作者在人脸数据集上进行了孤立训练。
作者在Flickr-Faces-HQ (FFHQ)人脸数据集上进行了训练,并在测试集上取得了高达81%的精度,并利用手性特征聚类对人脸中的视觉手性现象进行了初步的探讨:

1) 刘海分界处:人们一般用右手来分理刘海,这会导致刘海的朝向向一侧偏移,并出现视觉手性现象。
2) 眼睛:人们在看向物体时倾向于用一只主视眼进行瞄准,这样会导致人们的目光在进行拍摄时出现偏移。多数人的主视眼为右眼,而这一现象可能是导致视觉手性现象的成因。
3)胡子:与头发一样,可能与人们习惯于用右手理胡子有关。
作者提到,文中对以上的视觉手性现象的讨论均为初步的分析,而人脸中任有大量的视觉手性线索值得被发掘。
五、数字图像处理
作者对数字图像处理过程,例如去马赛克(最常见为Bayer Demosaicing)和图片压缩(最常见为JPEG Compression)过程中产生的视觉手性现象进行了分析。举个例子,当作者首次利用神经网络在Instagram数据集上进行自监督训练时,发现没有使用随机剪裁(random cropping)的神经网络尽管精度更高(在测试集上高达92%),但在部分图片上,类激活映射所得到的热图更着重关注图片的边缘部分,如左下图所示:

而在使用随机剪裁之后,我们得到的新的热图则更关注来自于图片中物体本身的线索(例如图中的衬衫领子)。作者推断这是由于Instagram的图片均为JPEG格式,经过了JPEG图像压缩这一数字图像处理方式。JPEG压缩的算法是在图片上对于每16乘16的像素格进行分别处理的,而对于不能被16整除的图片,其边缘会用统一方式进行处(例如重复边缘像素)。这会导致JPEG压缩的图片的边缘失真(edge artifact),从而导致了视觉手性现象。
作者通过概率论与群论(group theory)对数字图像处理过程产生的视觉手性现象进行了数学论证,并通过神经网络实验验证了这一现象在互联网图片中广泛存在。而此类的线索往往不能被肉眼可见,却在图片中存在固定的模式,因而为图像识伪的应用创造了可能性。
由于文中的证明和实验过程较为复杂,此处我们先给出数学定义和最重要的几点结论。
1、定义
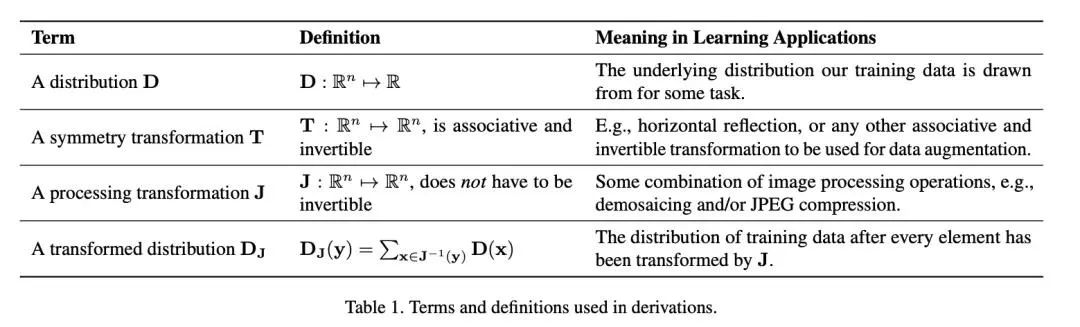
D为数据集所来源于的图像分布。T为一个图像变换函数,例如镜像翻转。需要注意的是论文中的证明不仅限于镜像翻转,也可以被用于任何具备结合律(associativitive)和可逆性(invertible)的变换。J为一个图像处理函数。例如去马赛克以及JPEG图片压缩。

为经过J处理后所得到的的新图像分布。
我们沿用之前对视觉手性的定义:对于任意图片x,如果D(x)= D(T(x)),那么D不具备视觉手性。对于任何经过数字图像处理的图片y,如果
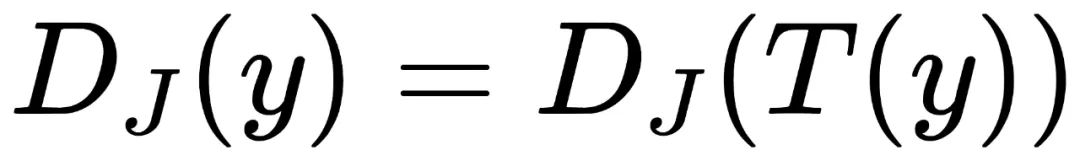
,那么

同样不具备视觉手性。
文中最重要的结论是:
当图像变换函数T和图像处理函数J具备交换律(commutative property)时,如果原先的图像分布D没有视觉手性,经过数字图像处理后的分布DJ也不具备视觉手性。换句话说,我们可以通过检查T和J的交换律,来判断数字图像处理能否造成视觉手性现象。
作者在论文中主要涉及了两种最常见的图像处理方式:
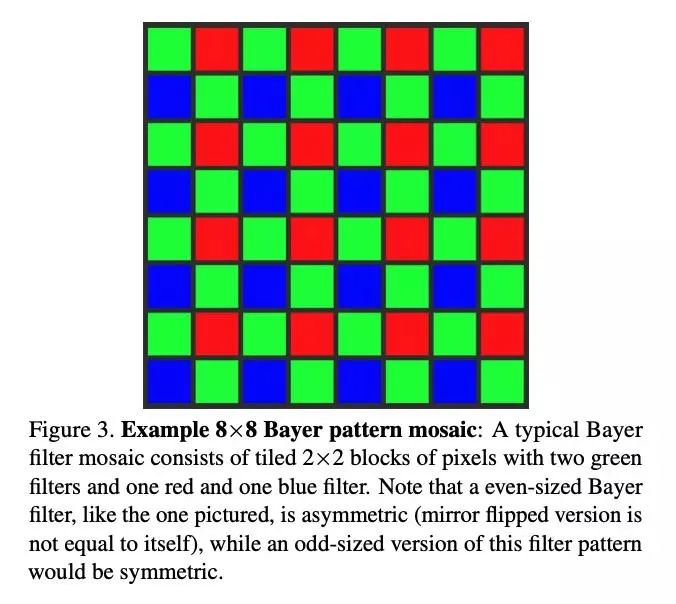
去马赛克(Demosaicing):数字相机的感光元件一般只能在每个像素格上捕捉RGB中的其中一种颜色,而其中最常用的为贝尔滤色镜(Bayer Color Filter Array),如下图所示。去马赛克则是将感光元件得到的二维图像还原为三维全彩的这一过程。
JPEG压缩算法(JPEG Compression):JPEG是一种有损的图像压缩方式,被广泛应用在如今大量的互联网图片上。一般以每16乘16的像素格为单位通过色彩空间变换,缩减像素采样,离散余弦变换等步骤来进行图片编码压缩。
2、结论
去马赛克或JPEG压缩算法单独使用时,会在特定的图片大小产生视觉手性现象。对于去马赛克,由于贝尔滤色镜为2乘2的像素格,且滤色镜本身不对称(参考上图绿红蓝绿的排序),任何能被2整除的图片宽度均会导致视觉手性。对于JPEG压缩,任何不被16整除的图片宽度均会导致视觉手性。这意味着,当去马赛克和JPEG压缩被共同使用时,任意宽度的图片都将产生视觉手性,因为同时满足不被2整除和能被16整除的数字不存在。当使用随机剪裁(random cropping)时,去马赛克或JPEG压缩单独使用并不产生视觉手性现象。当使用随机剪裁(random cropping)时,去马赛克和JPEG压缩同时使用将会产生视觉手性现象。这意味着互联网图片中可能存在大量有规律的,肉眼不可见的视觉手性线索,而人们将能够利用这类线索来进行图片识伪。
3、证明
那下面我们进入证明部分(读者需要对群论(Group Theory)有一定基础)文中最重要的证明为附加材料中的命题3:

命题3:当原图像分布D不具备视觉手性时,如果图像处理函数J与图像变换函数T具备交换律,则经J处理后的图像分布DJ也不具备视觉手性。
证明:由于T具备可逆性和分配律,T可以将原分布中的图片分为一个个不相交的循环群(disjoint cyclic groups)。
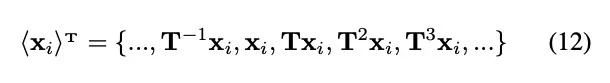
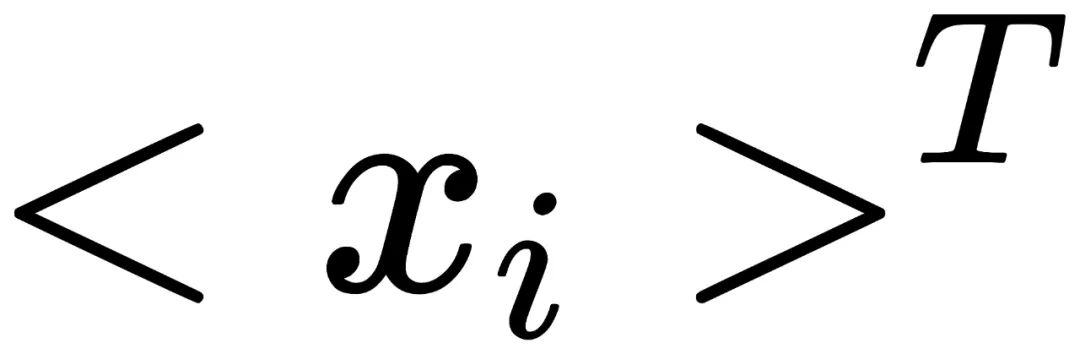
即为一个循环群,而这个循环群的单位元(identity element)可以选这个集合里面任意一个元素。这些循环群的群运算(group operation)可以被定义如下:
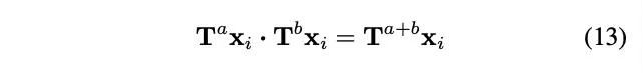
每个循环群的阶(order of group)由T以及其中的元素决定。举个例子,如果T为镜像翻转,那么对于一张对称的照片
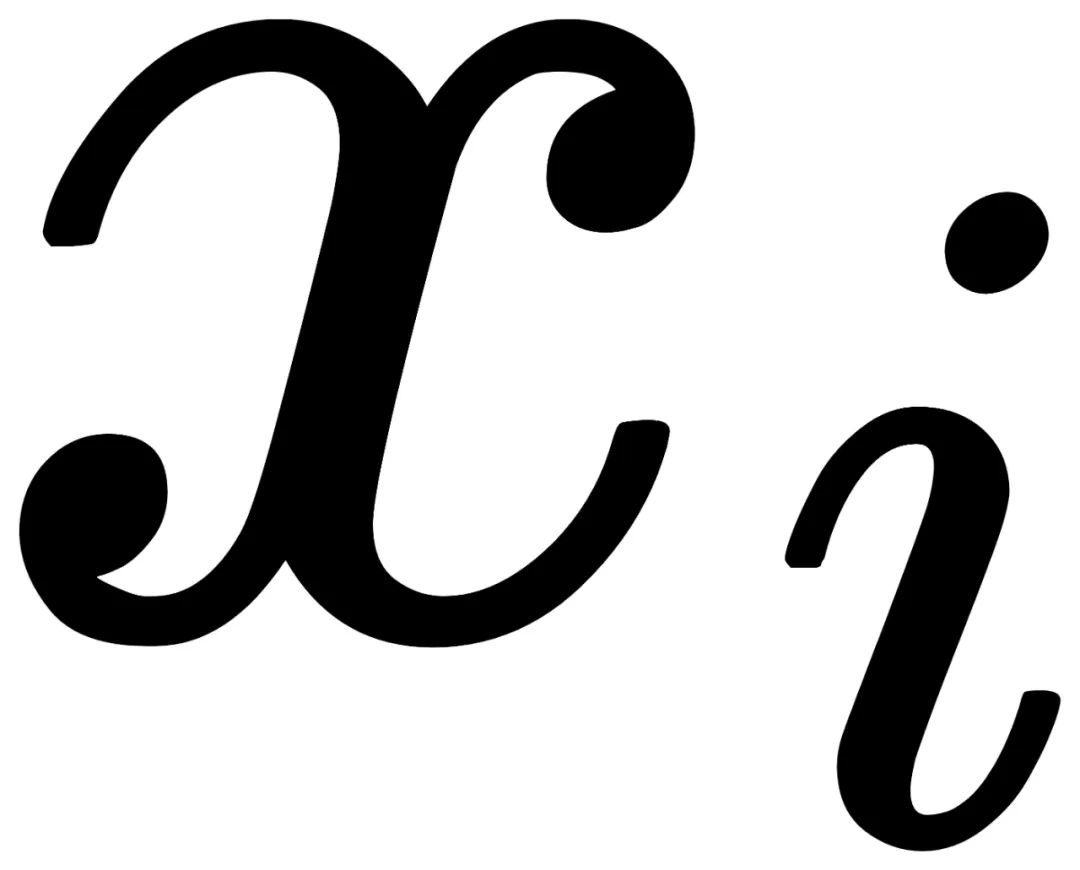
,其所在群的阶为1
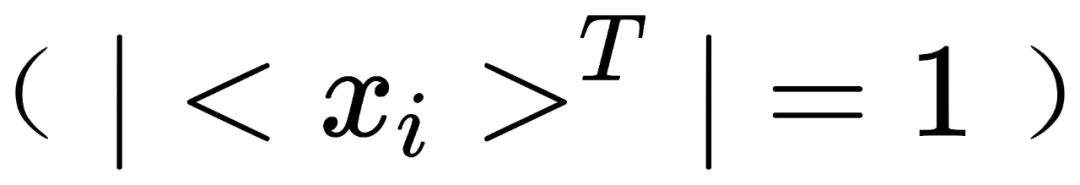
。对于不对称的一张照片
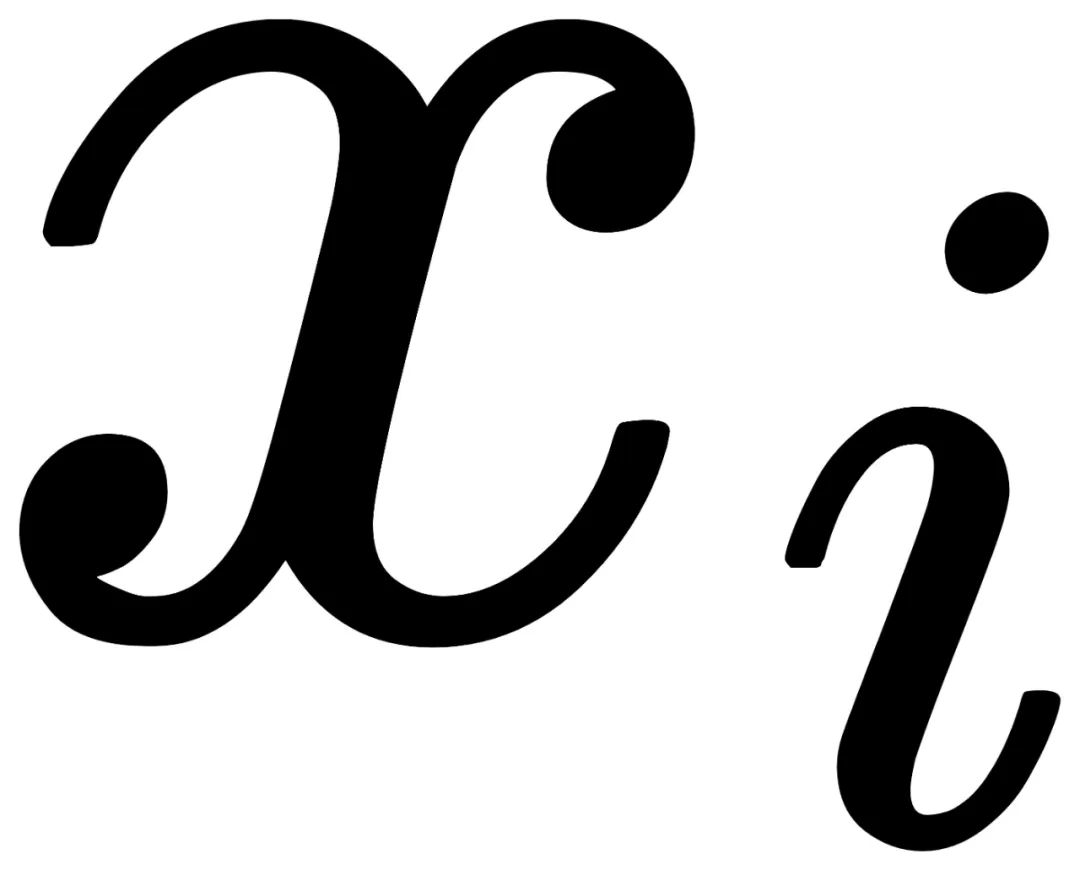
,其所在群的阶为2。
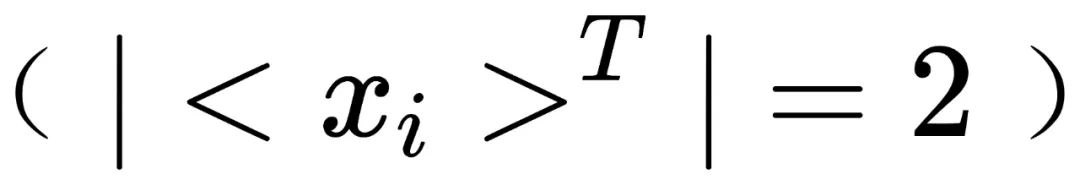












 分享
分享















发表评论
请输入评论内容...
请输入评论/评论长度6~500个字
暂无评论
暂无评论