CVPR 2020 最佳论文提名 | 神经网络能否识别镜像翻转
经过图像处理后，每个循环群
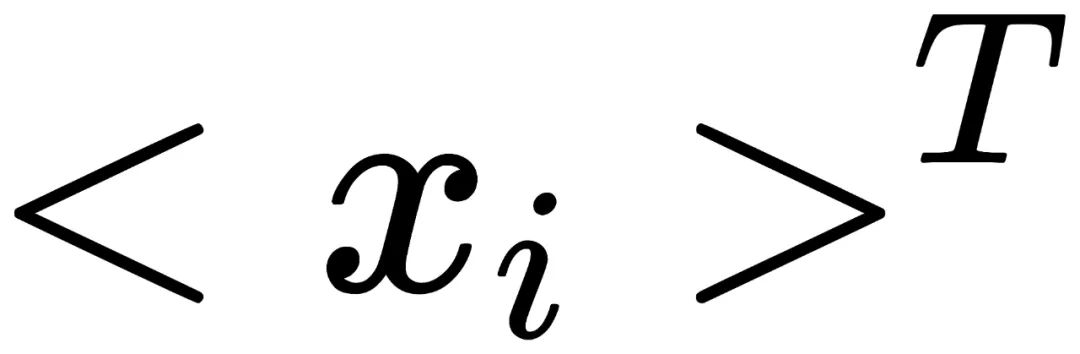
将变化为
：
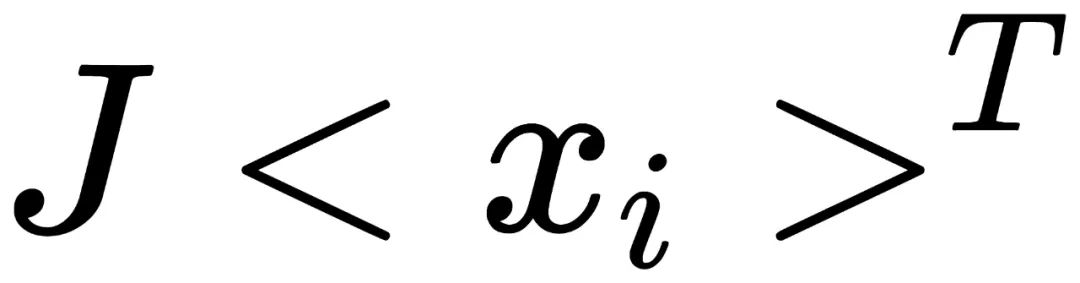
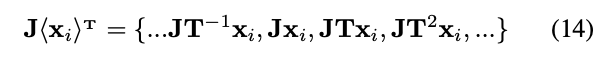
命题3里，我们假设T和J具备交换律，那么我们可以将上面的公式改写，并得到
：
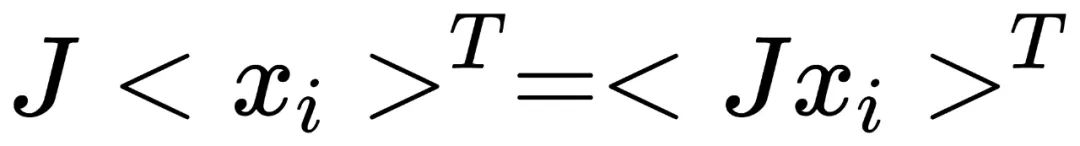
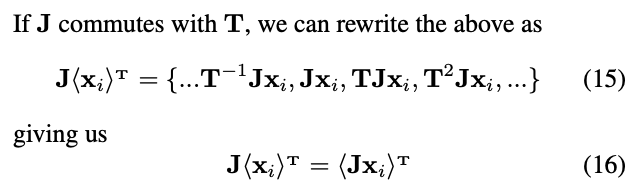
原分布D不具备视觉手性意味着：每个循环群
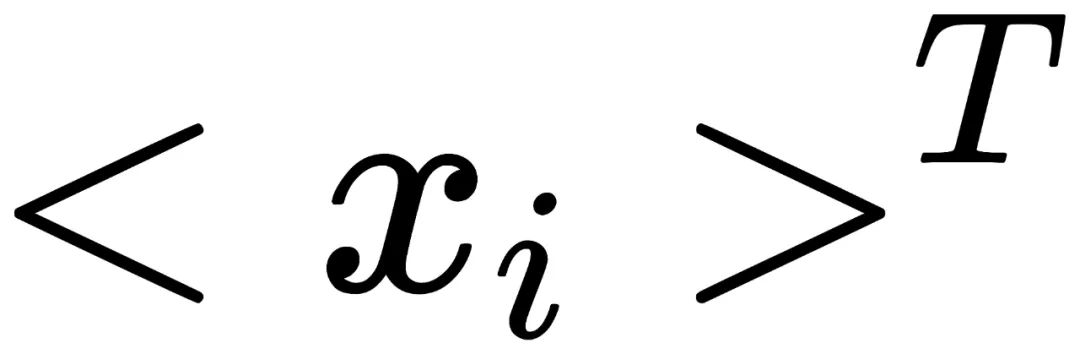
中的元素都有相同的概率出现。因此，由于经过J图像处理后循环群变为了
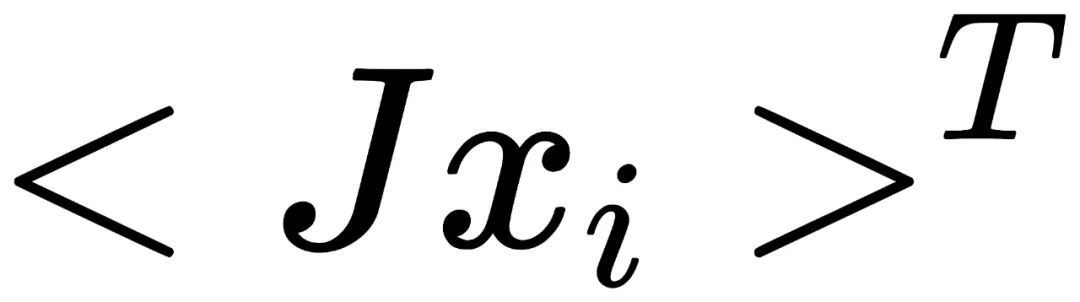
，我们只需要证明以下运算为同态（homomorphism）：
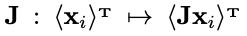
因为对于同态来说，根据第一同构基本定理（First Isomorphism Theorm）可以推理出每个输出对应着相同数量的输入。而因为每个循环群中单个输入
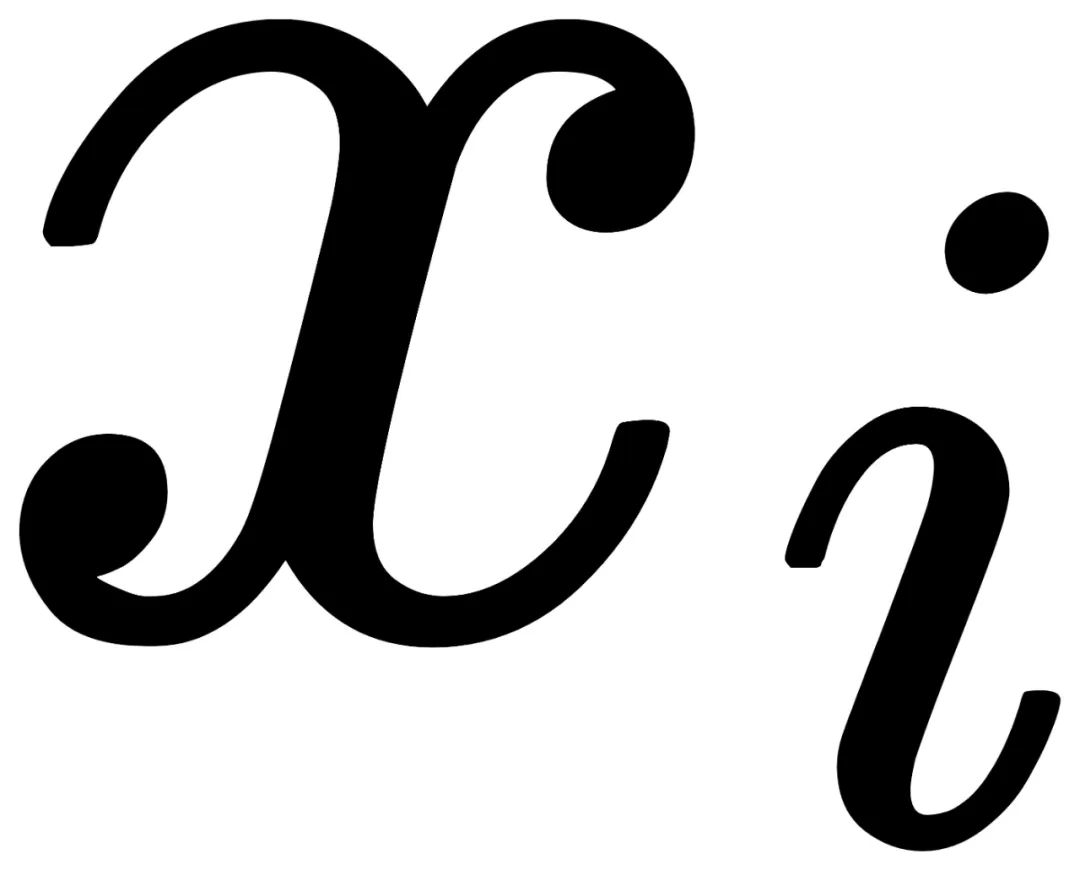
在原分布D上有着相同的概率，意味着每个输出
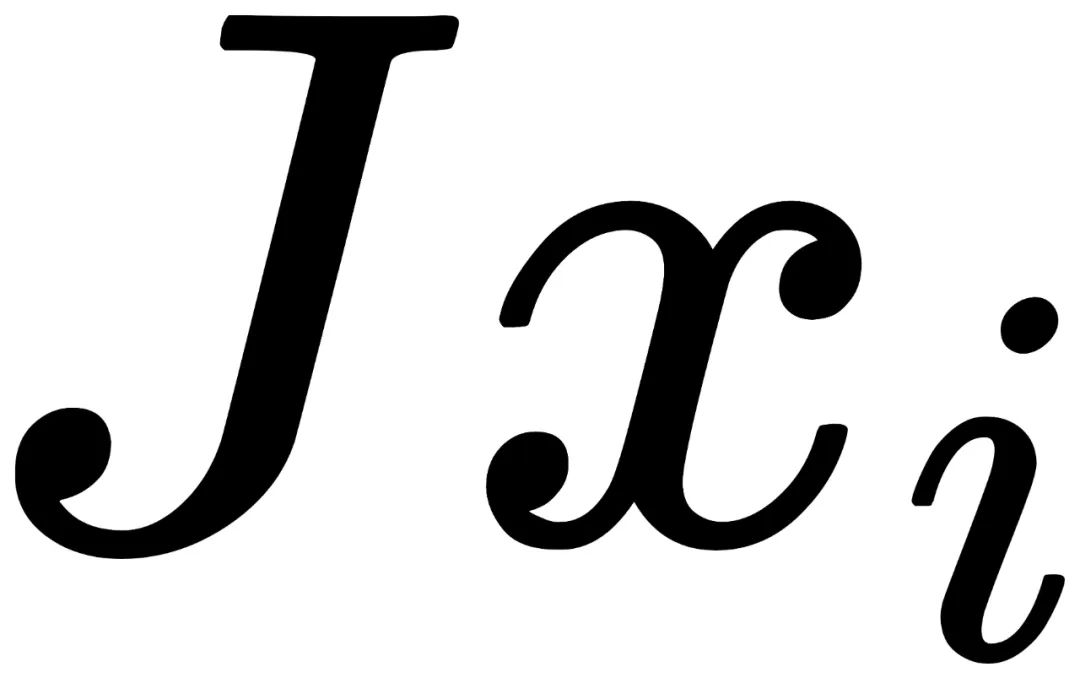
也具备相同的概率，也意味着
不具备视觉手性。证明同态的步骤如下：
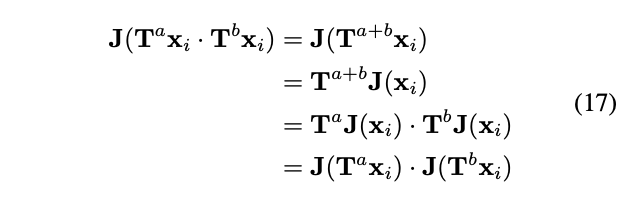
以上为命题3的证明。通过命题3，我们知道了J和T的交换律与处理后图像分布的视觉手性的关系。那么，只需要通过检查交换律，我们便可以判断图像处理是否可能产生新的视觉手性。检查的方式也很简单，对于任意图片x，我们只需要计算其交换残差（commutative residual）是否为0：
下图形象的解释了交换残差的计算过程：
文中使用去马赛克、JPEG压缩、以及两者结合这三种图像处理方法，对于镜像翻转这一图片变换方式分别计算了交换残差。
当去马赛克处理的图像宽度为奇数时，处理后的图像分布可能具备视觉手性；反之如果为偶数，则不具备视觉手性。当JPEG压缩的图片不为16整除时，处理后的图像分布可能具备视觉手性，反之则不具备。当两者结合后，处理后的图片一定具备视觉手性：
作者为了验证这些结论，在原本不具备视觉手性的人工数据集（高斯分布生成的随机图片）上，对不同宽度的图片分别进行了这三种处理，并使用神经网络进行了自监督学习。实验结果符合这一测试的预期。因为大量互联网图片都经过了去马赛克和JPEG压缩，这一结论意味着数字图像处理所带来的视觉手性现象在互联网图片中广泛存在。
当加入随机剪裁（random cropping）后，我们还能得到这一结论么？作者的答复是肯定的。
为了理解随机剪裁对于视觉手性的影响，作者提到了两个关键点。
第一点：命题三中只讨论了单种J的情况。而随机剪裁可以被视为许多种J（例如
是向右平移一格并剪裁，
是向右平移两个并剪裁）的结合，每一种有相同概率出现。
第二点：命题三中并没有讨论T和J不具备交换律的情况。例如当J是向将图片右平移十个像素并进行一次中心剪裁时，T和J无法具备交换律。在这种情况下，新的图像分布并不一定具备视觉手性。
对于第一点来说，假设我们有多种不同的J（例如
，
，
），而他们分别与T具备交换律时，我们可以用以下公式表达新的图像分布：
分享
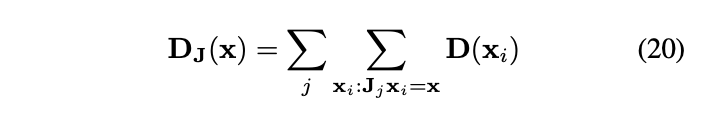
最新活动更多
-
11月28日立即报名>>> 2024工程师系列—工业电子技术在线会议
-
12月19日立即报名>> 【线下会议】OFweek 2024（第九届）物联网产业大会
-
即日-12.26火热报名中>> OFweek2024中国智造CIO在线峰会
-
即日-2025.8.1立即下载>> 《2024智能制造产业高端化、智能化、绿色化发展蓝皮书》
-
精彩回顾立即查看>> 2024 智能家居出海论坛
-
精彩回顾立即查看>> 【在线会议】多物理场仿真助跑新能源汽车
推荐专题
发表评论
请输入评论内容...
请输入评论/评论长度6~500个字
暂无评论
暂无评论